Table of Contents
ToggleDividing numbers can sometimes feel tricky, especially when fractions are involved. One common question that arises is how to calculate 1 divided by 1/2. This seemingly simple operation reveals a fascinating aspect of mathematics that can help clarify the relationship between whole numbers and fractions.
When dividing by a fraction, the process involves multiplying by its reciprocal. Understanding this concept not only simplifies calculations but also enhances one’s grasp of mathematical principles. As we explore this division, readers will discover that 1 divided by 1/2 equals 2, shedding light on the beauty of numbers and their interactions.
Understanding Division
Division serves as a fundamental operation in mathematics, breaking quantities into equal parts. Understanding division, especially with fractions, enhances numeric proficiency and problem-solving skills.
What Is Division?
Division represents the process of determining how many times a number (the divisor) fits into another number (the dividend). For example, in the expression “1 divided by 1/2,” 1 is the dividend, while 1/2 is the divisor. Performing division often involves rephrasing into multiplication by a reciprocal, simplifying calculations while keeping results accurate.
The Concept of Fractions
Fractions express parts of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). In the fraction 1/2, 1 indicates a single part, while 2 identifies the whole as being divided into two equal parts. Understanding fractions facilitates various arithmetic operations, including division, as it expands the scope of numbers beyond whole integers. This comprehension is vital when encountering problems requiring division by fractions, such as transforming 1 divided by 1/2 into multiplication of 1 and the reciprocal of 1/2, yielding the result of 2.
The Calculation of 1 Divided by 1/2

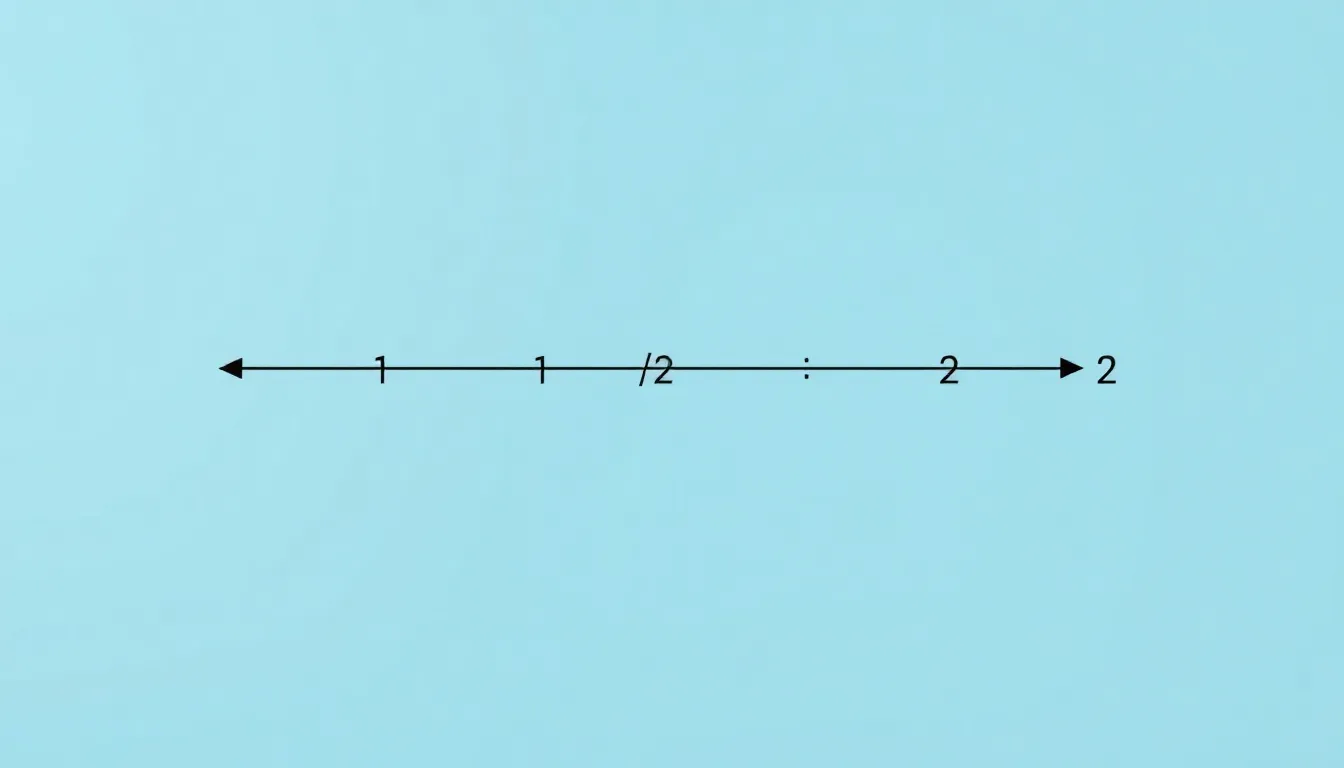
Dividing 1 by the fraction 1/2 demonstrates an important mathematical concept. This process involves multiplying by the reciprocal of the fraction.
Step-by-Step Calculation
- Identify the fraction: The fraction to divide by is 1/2.
- Find the reciprocal: The reciprocal of 1/2 is 2.
- Multiply: Multiply 1 by 2, resulting in 2.
The calculation simplifies to:
1 ÷ 1/2 = 1 × 2 = 2.
Visual Representation
A visual representation can clarify the division concept. Using a number line can illustrate the process:
| Number Line | Position |
|---|---|
| 0 | Start |
| 1 | Dividend |
| 1/2 | Divisor |
| 2 | Result |
On the number line, moving from 0 to 1 indicates the dividend. When dividing by 1/2, it shows how many halves fit into 1, resulting in 2, as each movement of 1/2 brings the total to the final outcome of 2.
Real-World Applications of 1 Divided by 1/2
Understanding the concept of 1 divided by 1/2 extends beyond the classroom. This mathematical principle finds relevance in numerous everyday situations and practical applications.
Using Division in Everyday Life
Division plays a crucial role in various daily tasks. When he or she needs to determine how many equal servings can be made from a certain amount of food, division simplifies the process. For instance, if a recipe calls for 1 cup of sugar and is intended to serve two people, one can identify that each person receives 1/2 cup. When scaling recipes for larger gatherings, such as a party for 10, calculating serving sizes requires division, demonstrating the utility of understanding fractions and division.
Practical Examples
Practical scenarios showcasing the division of 1 by 1/2 include:
- Dividing Items: When splitting a single item among multiple people, such as 1 pizza, he or she can divide it into halves, yielding 2 pieces.
- Budgeting: When managing finances, if an individual has $1 to spend on snacks at a party, and each snack costs $0.50, he or she can purchase 2 snacks.
- Time Management: In scheduling, if a meeting requires 1 hour and needs to be divided into 30-minute segments, division reveals that it accommodates 2 segments within that hour.
These examples illustrate how division not only facilitates everyday decisions but also emphasizes the importance of grasping fundamental mathematical concepts like dividing by fractions.
Common Misconceptions
Misconceptions about dividing by fractions often arise due to the complexity of fractional mathematics. Understanding these misunderstandings can improve overall numerical proficiency.
Misunderstanding Division with Fractions
Many believe that dividing by a fraction results in smaller numbers. In fact, dividing a number by a fraction increases the value. For example, when dividing 1 by 1/2, the operation essentially asks how many halves fit into 1. This challenge indicates that 2 halves fit, creating the result of 2. This misunderstanding stems from conflating division with subtraction rather than recognizing the operation’s fundamental nature of determining groups.
Clarifying Misinterpretations
Common misinterpretations include assuming that dividing by a fraction eliminates the fraction from the calculation. The correct approach involves multiplying by the fraction’s reciprocal. For instance, dividing 1 by 1/2 translates into multiplying by 2, leading to a clearer, more accurate result. This misconception hinders comprehension and can confuse students when they encounter more complex fraction operations. Ensuring clarity about this fundamental principle enhances both understanding and application in diverse mathematical scenarios.